Decoding the secret under the lens of mathematics and science
##This article can be read in pdf format attached here, which has proper meetei mayek font Ama and associated mathematical equations. The Untold Meaning of Sanamahi Symbol_05_07_2022

By Raghu Ningthoujam
Dear learned readers, are you ever aware of the holy symbol of Sanamahi? What is that sacred symbol which can represent the supreme God Lainingthou Sanamahi and what is the specialty of that divine symbol of the ultimate God Lainingthou Sanamahi? Where was the pristine symbol of Lainingthou Sanamahi kept hidden for centuries?
Yes, Lainingthou Sanamahi has a spectacular holy symbol as shown in figure. The holy symbol is called Ama (the One) as found in holy Meetei Puya -“Wakoklon Heelel Thilel Salai Amailon Pukok Puya” (hereafter known as Wakoklon puya) and will appear very often in the article. The divine symbol of God is so special, having its mathematical beauty and scientific essence. However, for centuries, the sacred symbol of Lainingthou Sanamahi was lying unknown of its hidden meaning, in the Wakoklon puya. This article will bring out the untold meaning of the holy Sanamahi symbol and its divineness by unravelling the underlying secret of the Sanamahi symbol and will solve the centuries-old enigma of Puya under the lens of mathematics and science.
Thus, let’s have a look at the excerpts of Wakoklon Puya that what have been written in the Puya about Ama – the symbol of the supreme God – Lainingthou Sanamahi, followed by the corresponding English translation of the original Puya excerpts.
Original Puya – in Verbatim
Tingpalpaki Mapu Ipungo Eepung Loinapa Apakpana Talang Oina Leilingei | Tingpalpa Amaki Ma-ongpu Leptalingei | Mei | Eesing | Nungsit | Numit | Tha | Thouwaimichak | Amam Angan Khaitalingeita Pumnamakna Leitali-ngeita Mathanna Onna Onna | Talang Malang Oina Sai-ontuna Leilingeita | Talang Atingpapu Eepung Loinapa Apakpana | Talang Malang Eem Oina Haina Humna Asumna Leilingeita Malem | Nongthou Manung Oinapa Semke Ninglakle | Ama Hailipa Mapuna Talang Malang Oina Haina Humna Leilingeita | Mapu Sitapaki Nungpung Wakhanna Eenung Pungta Lupkhituna Malem Leisapu Phukkhat Chingkhat Thangkhatlakpa Matamta Eenungpungki Sai-Onna Kampi | Laicha | Malangpa Chongthokle…..
Ama Hailipa Eepung Loinapa Apakpana Thouwaimichak Cheiyom Taletpu Eenunglon Khununglonna Cheiyon Talet Haina Haikhale…..
Tingpanpa Ama Ki Kayatki Laimingpu Taipangpanpa Ama Ki Kayatta Eenunglon Khununglon Ki Eenung Eeyek | Khunung Eeyek Haina | Eeyek Eepi Laiyek Asiki Wali Likhunpu Khakpane…..
Eepung Loinapa Apakpana Eeyek 18 Amati Shingthalon Cheising Eeyek Ama Ta Saiontuna Ating-Aa Sitapa Ahangpa Haina Koukhale | Eeyek Asipu Eenunglonna Ama Kouye | Khununglon Khonthok Eewai Eeninna Ating-aa Haina Koukhale…..
Eepung Loinapa Sitapa Mapuna, ….. Lainingthou Salailen Sitapaki Mafamta Talang Laipau Pituna | Numit Humni Supaki Angangki Matam Kumna Sanaki Masak Manpa Nouwa Ama Oina Leilamke | Ei Asipu Nahakki Nachaa Makni Ningtuna Eipu Yoklo || ….. Laipaoki Likhun Liklampu Laiyamsingna Tachakhi ||o|| Asum Oipa Laipaoki Matung-inna Sitapaki Eesaifu Eelon-nungta Numit Humni Supaki Nouwaki Mawong Oina Sanaki Machu Manpa Nouwa Ama Leilamle || Nouwa Atupu Yenglaka Sanaki Masak Manpa Angangpa Machuna Leitengpa Mahi Atupu Upata Sanamahi Haipa Mingthonpu Pituna Machaki Matamkumna Loukhatle || …..
English Translation
The first quotation of the Puya states that “In the very beginning, when there was nothing in the cosmos, when there was no form of the universe (Tingpalpa), no fire, no water, no air, no sun, no moon, no star, no light and no darkness; there was a Supreme God, the owner of the universe (Tingpalpa Mapu) called “Eepung Loinapa Apakpa” in talang form, alone in the entire fabric of space-time. When the supreme God, the ultimate owner called Ama (the ONE) was there freely in the talang-malang form, by His desire, He created the universe, earth, sky, fire, water, air and everything.….”
The second quotation of the puya says that Ama (the ONE) aka Eepung Loinapa Apakpa, the universal God, has called the seven star cheiyom as the seven weeks, by both God (eenunglon) and human beings (khununglon)…..
The third quotation of the puya says that “The 18 alphabets of Meetei scripts have been derived from the anatomy of the One God (Ama) aka Eepung Loinapa Apakpa, the ultimate God, the owner of the cosmos…..
The fourth quotation of the puya states that the universal God “Eepung Loinapa Apakpa” has incarnated to the 18 primary alphabets (eeyek eepi) of Meetei script and the Shingthalon Cheising eeyek (the mathematical numeral figure) Ama (the ONE), and has been known as Himself Ating-nga sitapa ahangpa (the sky, the deathless void), which is represented by Ama (the One), by God (eenunglon) and Ating-nga alphabet by human beings (khununglon),…..
The fifth quotation of the puya says that “The Supreme God and deathless Eepung Loinapa Sitapa pervaded in the vastness of cosmos; in order to search the path to Him and to know that He is there, He gave a message from space (talang laipao) to Lainingthou Salailen Sitapa that ‘I will be there like a child who will be in his prime of three-day old, You (Salailen Sitapa) bring me up as your own child. Thus, according to the message from God, in the pool of liquid inside the Isaiphu of (Salailen) Sitapa, there found a child who was in the form of a three-day old child, Salailen Sitapa embraced the child and named the child as ‘Sanamahi’…..
Towards the Symbol of Sanamahi
From the above Puya verses and the corresponding English translations, we know that before anything existed in the universe, a supreme God Eepung Loinapa Apakpa existed freely in talang-malang form with infinite degrees of freedom in the entire cosmos, as the owner and guardian of the seed of the universe. The supreme God Eepung Loinapa Apakpa, by His desire, created the universe and everything inside it, from the seed universe. The seed universe was the (initial) singularity of the entire space-time and the supreme God Eepung Loinapa Apakpa was the owner (Father) of that baby (seed) singularity and hence He is known as Tingpalpaki Mapu (Owner of the Universe, Tingpalpa means Universe, Mapu means Owner) or the Supreme Singularity to which everything belongs, i.e. even the universe, even the baby (seed singularity). This baby singularity is what is called the Big Bang Singularity in modern science. We’ll answer later what the Supreme singularity is.
The ultimate God Eepung Loinapa Apakpa is also known as Ama (the One) and He stands in the form of a figure Ama – the numeral figure One in Kanglei Meetei scripts. Eepung Loinapa Apakpa has embodied to the numeral figure Ama (the One) along with the 18 primary alphabets (eeyek eepi) of Meetei script. And, Eepung Loinapa Apakpa, by His desire, has incarnated Himself as a three-day old child called Sanamahi to Lainingthou Salailen Sitapa. Thus, it is very clear that the figure Ama (the One) is the holy symbol of the creator Eepung Loinapa Apakpa and hence the symbol of Sanamahi.
Why is this symbol Ama for Sanamahi !
What is the speciality and divineness of the symbol Ama (the One) which represents Lainingthou Sanamahi, as clearly mentioned in puya, as a centuries-old puzzle to us. Lainingthou Sanamahi is the ultimate, supreme God, the creator of the universe, human beings and all life and lifeless forms in the universe. There is nothing above to Sanamahi as per Meetei doctrine and religion. Then, there must be something unique for this symbol Ama, otherwise a mere symbol cannot represent a Creator. The learned readers will come to know that the pristine symbol Ama is equally as fascinating as Sanamahi – the creator. deciphering the secrets and the speciality of the pristine symbol Ama, is the subject of the subsequent sections. However, before we discover the underlying secret and beauty of Ama, let’s first have a look at the amazing stuffs called – Fibonacci Numbers, Golden Ratio, Golden Spiral, Fibonacci Spiral etc. which will ultimately lead to bringing out various facets of the holy symbol and understanding the article.
Fibonacci Numbers (Fn)
This fabulous sequence of numbers was discovered by great Italian mathematician – Leonardo of Pisa, later known as Fibonacci (1170-1250 AD), in his book called Liber Abaci, published in 1202 AD.
Fibonacci Sequence is an infinite series of numbers. Given the first two initial numbers – 0 and 1, each new number in the series is the sum of the two previous numbers. Mathematically, the nth term of the Fibonacci series Fn can be written as the sum of its previous two terms i.e. (n-1)th and (n-2)th terms, as given in the following Recursion relation:
Fn = Fn-1 + Fn-2 for n = 2,3,4,…., with F0=0 and F1=1
Or
Fn+2 = Fn + Fn+1 for n = 0,1,2,3,4……, with F0=0 and F1=1
Given the first two terms of the series as 0 and 1, third number of the series is 1 = 0+1; fourth number is 2=1+1; fifth number is 3=1+2and so on. Thus, we get an infinite series of numbers called Fibonacci series as follows:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, … and it continues forever.
The numbers in the series are called Fibonacci numbers and the Fibonacci series continues forever. At first glance, there is nothing spectacular about these numbers beyond the relationship that would allow us to generate additional numbers of the sequence quite easily. However, the Fibonacci numbers are turned to be very amazing number found in nature with a myriad of applications and appearances in almost every part of nature and branches of science, as it can be seen in subsequent sections.
Depending on conventions, learned readers may find different forms of Fibonacci sequence and recursion relations accordingly. The differences in the sequence comes in the beginning terms either it starts with 0 or 1, after which the remaining numbers of the sequence remain same. Some scholars omit 0 in the first term and begin with 1 and followed by 1 as 2nd term. Omission of 0 as the first term is probably to avoid division by 0 while taking ratios of consecutive Fibonacci numbers. Accordingly learned readers may encounter the following Fibonacci sequence as well:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, … and it continues forever.
The corresponding recursion relation is:
Fn = Fn-1 + Fn-2 for n = 2,3,4,5,…., with F0=1 and F1=1
Or
Fn+2 = Fn + Fn+1 for n = 0,1,2,3,4…, with F0=1 and F1=1
Though there are different conventions and forms of Fibonacci sequence, fundamental property of Fibonacci series remains same i.e. given first two terms of the series, every number in the sequence (after the first two) is the sum of the two preceding numbers. In the present article, the writer will maintain the original form of Fibonacci series starting with 0 and 1.
Golden Ratio (Phi )
Golden Ratio is yet another fabulous number which has intrigued mathematicians, philosophers, scientists, artists, designers over generations to generations. Golden ratio can be defined both from geometrical point of view and Algebraic point of view as well. However, whatever way the Golden is defined either geometrically or algebraically, the ratio remains the same and it turns out that golden ratio is the positive root solution of quadratic equation of general form x2-x-1=0. Golden Ratio is also known by extreme and mean ratio (Euclid), Golden Section, Golden Number, Divine Proportion etc.
Whether Golden Ratio Phi was known to mankind since time immemorial is a question of debate. However, the first written record of golden ratio was found in 300 BC in the masterpiece geometrical book called ‘Elements’ written by Greek great mathematician Euclid as a proposition in his book, which reads as – “A straight line is said to have been cut in extreme and mean ratio when, as the whole line is to the greater segment, so is the greater to the lesser”.
Algebraically or in more general way, in mathematics, two numbers (say a and b, a>b) are in Golden Ratio if the ratio of the larger number to the smaller number (i.e. a/b) is same as the ratio of the sum of the numbers to the larger number (i.e. (a+b)/a). This can be expressed as follows:
(a/b) = (a+b)/a for a>b, which can be written as a = √ [b(a+b)]= Geometric Mean of b and (a+b)
Let’s take the common ratio as x. Now,
(a/b) = (a+b)/a = X which gives the famous golden ratio equation
X2-X-1=0, It is a quadratic equation in x and on solving, the positive and negative roots of the quadratic equation are –
X+ = (1+√5)/2 » 1.618…. = Phi (Capital called Golden Ratio)
X– = (1-√5)/2 » 0.618…. = Reciprocal of Golden Ratio Phi
Historically, positive root of extreme and mean equation is called Golden Ratio and is denoted by Greek Capital letter Phi, in honour of the greatest Greek Sculpture Phidias (ca. 490-430BC), that is believed that Phidias has used Golden ratio proportions in his master sculptural works during his time. By standard convention, capital Phi = 1.618… is called golden ratio and its reciprocal Small phi = 0.618… is called Silver ratio. However, again, based on convenience and convention, some scholars take smaller phi = 1.618…as the Golden Ratio and Capital Phi = 1.618…as Silver Ratio.
What makes the ratio golden strange and what is the speciality of the ratio! Golden ratio Phi has unique characteristic that it is the ONLY number for which following relations are true i.e. (i) Product of a number and its reciprocal is 1 and (ii) Difference of a number and its reciprocal is 1.
From equation (Phi)2 = 1+ Phi which can be written in Pythagorean form as (Phi)2 = 12+ (√Phi)2, the triangle which satisfies this relation is called Kepler triangle and apparently this Keplerian triangle property has been used in the construction of the Pyramid of Giza (built ~ 4500 years ago).
Also, from equation Phi = 1+ (1/Phi) and substitute Phi = 1+ (1/Phi) in the denominator Phi and continue the process forever, we get yet another beautiful express of Phi as infinite continued fraction:
Phi = [1;1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1………]
As it can be seen above that the golden ratio Phi is an irrational number – one that has an unending decimal value – one that has no repeating pattern. However, it turns out to be that golden ratio Phi is the ‘MOST irrational’ number among all the irrational numbers ever known. Numerically, golden ratio Phi is approximately equal to.
Phi = (1+√5)/2
» 1.6180339887498948482045868343656381177203091798057 (up to 50 digits) ……………………..infinity, which we approximate to 1.61803
And, numerically, the reciprocal of golden ratio (1/Phi) is approximately equal to:
phi = (1-√5)/2 = Phi -1
≈ 0.6180339887498948482045868343656381177203091798057 (up to 50 digits) …………………to infinity, which we approximate to 0.61803
Thus, Phi = (1+√5)/2 » 1.6180 (Golden Ratio Phi) and
1/Phi = phi = (1+√5)/2 » 0.6180 (Silver Ratio phi)
Binet’s Formula
Having discussed Fibonacci series and Golden ratio in the above sections, now, let us see the relation between them. Interestingly, Fibonacci series can be derived from golden ratio and vice-versa. In the Fibonacci series, instead of adding the consecutive numbers, if we were dividing each consecutive Fibonacci number, the ratio (quotient) gradually converges to a number which is nothing but the Golden Ratio Phi ≈ 1.61803 (which we shall see mathematically soon).
The relation between the Fibonacci series and Golden Ratio is given by a beautiful formula called Binet’s formula, in honour of a French mathematician Binet who derived it in 1843. Binet’s formula says that if Phi and phi are the positive and negative roots of the characteristics equation of the golden ratio equation X2-X-1=0, then Nth Fibonacci number is given by:
FN = [(Phi)N – (phi)N] / (Phi – phi), for N > 0
Since Phi = (1+√5)/2 and phi = (1-√5)/2 and 1 + (1/Phi) = Phi, the above Binet’s formula can be written in various forms as follows:
FN = 1/(2N√5)[(1+√5)N – (1-√5)N]
In terms of only Golden Ratio F, Binet’s formula can be written as:
FN = [(Phi)N – {- (1/Phi)N}] / {Phi + (1/Phi)}
As mentioned above, ratio of the consecutive Fibonacci numbers converges to Golden Ratio Phi, which can be seen below, using the above Binet’s formula.
(FN+1) / (FN) = [(Phi)N+1 – {- (1/Phi)N+1}] / [(Phi)N – {- (1/Phi)N}]
As N® Infinity (¥) i.e. when the higher numbers in the Fibonacci series are taken), the 2nd terms in the numerator and denominator parts approach to zero and hence neglected. Thus,
Limit (N®¥) (FN+1) / (FN) = (Phi)N+1 / Phi)N = Phi (golden ratio)
This can be seen by taking consecutive numbers ratios (1/1, 2/1, 3/2, 5/3, 8/5,13/8,21/13,34/21,55/34,89/55,144/89,233/144,610/377,987/610,1597/987,2584/1597 and so on…………………… in the Fibonacci series i.e.
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, … and it continues forever.
The ratio gradually converges to golden ratio Phi ≈1.61803
Golden Spiral and Fibonacci Spiral
Before we come to Golden Spiral and Fibonacci Spiral, humble writer wants to introduce the concepts of Golden Rectangle, Golden Angle, and Logarithmic Spiral which will be required to understand the Golden Spiral and Fibonacci Spiral in a better and easy way.
As we have seen in the above sections that two quantities (say two numbers) are in golden ratio if the ratio of the two quantities (numbers) is equal to golden ratio Phi. An angle is said to be golden angle if a circle is divided in two arcs in such a way that the ratio of the major arc to the minor arc is in golden ratio. The golden angles of a circle are obtained by dividing 360 degrees by Phi (≈1.61803) ≈ 222.492 degree and the other pair of golden angle is (360 deg minus 222.492 deg) ≈ 137.508 degree. Historically, the smaller angle 135.508… is known as Golden Angle.
Similarly, a rectangle is said to be a golden rectangle if the ratio of its two sides is equal to golden ratio (i.e. Length/Breadth = Phi). An interesting property of a golden rectangle is that a golden rectangle can be subdivided into a square and another golden rectangle. If L and B denote the length and breadth of a golden rectangle such that L/B = Phi, then the golden rectangle can be subdivided into a square of side B and another rectangle of length (L-B) and breath B, which turns out to be another golden rectangle. This smaller golden rectangle can again be subdivided into another square and another smaller golden rectangle, which can further be subdivided, ad infinitum, into even smaller but similar shapes. The resulting entity is self-similar. That is, if you zoom in on a smaller rectangle with even smaller rectangles and squares embedded in it and magnify it, it will look the same as the original, bigger rectangle. The property that an object will look the same at all scales is called Self-Similarity, a fundamental proper of Spirals.
A golden spiral can be drawn from the property of golden rectangle and self-similarity. As we have just seen that a golden rectangle can be divided into squares and smaller golden rectangles in an infinite way. To draw a golden spiral, we have to consider only the squares which have been divided from the respective golden rectangles. For each square, we can draw an inscribed quarter circle with radius equal to the side of that square. Then, by connecting all the inscribed quarter arc circles, we can get (draw) a spiral called the Golden Spiral.
On the other hand, a Fibonacci spiral can be drawn in the reverse way of drawing a golden spiral in the following way, from the Fibonacci series – 0,1,1,2,3,5,8,13,21……. The point is that to draw a Fibonacci spiral, we have to first draw Fibonacci squares whose sides are represented by the Fibonacci numbers and each square will have an edge that is the sum of the two squares before it (remember it is the fundamental property of Fibonacci sequence).
Thus, let us begin. It is convenient to draw in a graph paper having several squares in it. Therefore, take a graph paper and first draw the first Fibonacci square with the first Fibonacci number 1 as side of 1unit length. Then, adjacent to the 1st Fibonacci square, draw 2nd Fibonacci square with 2nd Fibonacci number 1 as side of 1 unit length. Then, adjacent to the 2nd Fibonacci square, draw 3rd Fibonacci square with 3rd Fibonacci number 2 as side of 2 unit length, in such a way that each square will have an edge that is the sum of the two squares before it. In this process, continue drawing 4th Fibonacci squares, 5th Fibonacci squares and so on…with the condition that each square will have an edge that is the sum of the two squares before it. Then, a quarter arc circles can be drawn (inscribed) inside each Fibonacci squares with radius equal to the side of each Fibonacci square. Then, by connecting all the inscribed quarter arc circles, we can get (draw) a spiral called the Fibonacci Spiral.
If we carefully observe the process of drawing the Fibonacci spiral, one can notice that by drawing the Fibonacci squares, starting from the centre (1st Fibonacci number), we are actually constructing bigger and bigger Golden rectangles, having corresponding squares in it, after every steps. This is in fact the reverse of what a golden spiral was constructed from golden rectangles.
That it, a Golden spiral is drawn spiralling in, from Golden rectangles by sub-dividing into squares and smaller golden rectangles and connecting the quarter arc circles of the squares. On the reverse way, a Fibonacci spiral is drawn spiralling out, from the Fibonacci squares by constructing to bigger golden rectangles (very near) and connecting the quarter arc circles of the squares. Thus, we can perceive that Golden spiral is winding in the limit to a point, which is fancifully called ‘the Eye of God’ while a Fibaonacci spiral is winding out from the centre.
Mathematics of Spirals
In order to comprehend the distinct mathematical differences between the Golden spiral and Fibonacci spiral, let us first understand what it is a Logarithmic spiral. The difference in simple words is that Golden Spiral is a special type of Logarithmic Spiral and Fibonacci Spiral is an approximation of Golden Spiral. That is golden spiral and Fibonacci spiral are similar, but not exactly same.
Mathematically, in polar coordinates (r,Theta), a logarithmic spiral has the equation: r = a Exp (b.Theta), where a = initial radius of spiral and b = growth factor of spiral.
In β denotes the arm-radius angle of the logarithmic spiral which is defined as the acute angle between the tangent to the spiral (curve) and the polar radius, the logarithmic equation can be written as r = a Exp (cot β. Theta), where b = cot β = constant.
Since the arm-radius angle is constant and it satisfies the equation, b = cot β, logarithmic spiral is also known as Equiangular Spiral.
A golden spiral is a special type of logarithmic spiral wherein the radius of the spiral increases by a factor of golden ratio (F) for every ¼ turn (Theta = Pi/2). That is Growth factor, b, is given by: b = {Loge(Phi)} / (Pi/2)
Therefore, the polar coordinate equation of the golden spiral is: r = a Exp [{2. Theta. Loge(Phi)} / Pi] or equivalently, r = a (Phi)^(2.Theta./Pi) from which it is inferred that for every ¼ turn that is Theta=Pi/2, radius of the golden spiral r = a.Phi that means radius increases by a factor of golden ratio Phi. Also, since b = Loge(Phi) / (Pi/2) and also b = cot β, the arm-radius angle β is constant for golden spiral and can be calculated as
β = arccot [Loge(Phi) / (Pi/2)] » 72.97 deg. = constant
Since the arm-radius of a golden spiral is also constant (»72.79o), golden spiral is also called an equiangular spiral like logarithmic spiral.
However, for a Fibonacci spiral, the arm-radius angle is not constant and it oscillates (periodic variation) continuously.
Also, for both the Golden spiral and Fibonacci spiral (curves), the curvature can be calculated and it is found that the curvature of golden spiral is continuous while the curvature of Fibonacci spiral is discontinuous.
Because of the constant growth factor and arm-radius angle, golden spirals have the property of self-similarity. That is, the shape is infinitely repeated when magnified. In general, a logarithmic spiral is a self-similar spiral.
From the Physics point of view, spirals are lowest-energy configurations which emerge spontaneously through self-organizing processes in dynamic systems and naturally most preferred state. From the chemistry point of view, a spiral can be generated by a reaction-diffusion process, involving both activation and inhibition.
Ideality Vs Practicality
As we have seen just above that, golden spiral is special type of logarithmic spiral whose radius either increases or decreases by a factor of the golden ratio Phi with each one-quarter turn and Fibonacci spiral is an approximation of golden spiral.
And also, we know that, the golden ratio Phi is the most astonishing number ever found and at the same time, it is also the most confusing number as well. The learned readers can find lots of confusions about the golden number Phi, mostly in its applications as golden spiral, but not its mathematical property. Mathematical properties of this beautiful number is accurately stated while the applications of the golden spiral are either wrongly stated or overstated. This confusion arises from the irrational nature of the number. As irrational number is not a natural number system and golden ratio Phi being the most irrational number, golden spiral which is associated with golden ratio Phi cannot be found be nature as such. Golden spiral is an ideal spiral and it can be found only mathematically. For practical purpose, and irrational number is transformed to its closest rational number and it approximated to certain digits.
Practically, golden spiral is manifested as Fibonacci spiral which is a very close approximation of the ideal golden spiral. Thus, Fibonacci numbers and Fibonacci spiral patterns are manifested in nature and profusely found in nature. However, point to be noted is that not all the spirals found in nature are Fibonacci spirals. The reason is simple and it lies with the origin of the Fibonacci series. If you remember, the Fibonacci series, on rabbit population growth, was derived from the ideal assumptions that no external influence, no environmental factors shall influence the population growth. Like no predators shall eat the rabbits, no rabbits shall die etc. However, when we talk about Fibonacci spirals in nature like in certain plants, certain animals, their growth factor which determines the shape of the spirals, may be influenced by certain environmental factors and the growth may be taking place under certain constraints like induced stress, then the shape of the spiral would deviate from the supposed-to-be proper Fibonacci spiral. Thus, all these parameters shall be taken into account while considering the applications of these beautiful spirals in nature as well as in ideal mathematical conditions.
Altogether putting in simple words, a golden spiral is ideal, mathematical spiral while a Fibonacci spiral is practical, nature spiral. Fibonacci spiral is approximation and manifestation of golden spiral in nature. Golden spiral and Fibonacci spirals are very similar but not exactly equal. Because the ratio of two consecutive Fibonacci numbers approaches the golden ratio, the Fibonacci spiral, as it spirals out, will eventually converge to the golden spiral and for practical purposes, the two spirals i.e. golden and Fibonacci spirals are synonymously used.
Myriad of Applications
There is plethora of applications wherein Fibonacci sequence, Golden ratio, Golden Spiral and Fibonacci spiral manifest themselves almost everywhere and have fascinated mathematicians, scientists, artists for many hundreds of years.
The number of petals in a flower often turns out to be one of the Fibonacci numbers: 3, 5, 8, 13, 21, 34 or 55… Famous examples include – the lily has three petals, buttercups have five, the chicory has 21, the daisy has often 34 or 55 petals, etc. Not only the number of petals in a flower, the number of leaves in a plant consistently follows Fibonacci sequence. In a plant, it is generally found that a new leaf advances by the same angle from the previous leaf and that angle between the successive leaves called divergence angle is usually close to 137.5 degree, which is nothing but the Golden angle. Fibonacci numbers in petals and golden divergent angle in Phyllotaxis (study of leaf arrangements in plants) appear on account of the ideal packing arrangement as selected by Darwinian processes and it allows the best possible exposure to sunlight and other factors. The Fibonacci sequence (golden ratio) can be seen in the spiralling patterns of sunflower seeds, pineapples, cauliflowers etc. The Fibonacci sequence can also be seen in the way tree branches form or split, roots systems and algae.
Golden Ratio and Fibonacci numbers are found to have manifested in the structure of human body and animals and they often appear in the face, body, fingers, teeth, anatomy, heart, lungs, uterus, and even down at our DNA – the genetic scale.
The human body is based on patterns of golden ratio Phi and the Fibonacci number 5 which is the basis for Phi as well. The Fibonacci number 5 appears as 5 appendages to the torso, in the arms, leg and head, 5 appendages on each of these, in the fingers and toes, 5 openings on the face, 5 sense organs for sight, sound, touch, taste and smell. Interestingly, golden ratio Phi is also intricately related to Fibonacci numbers 1,2,5 that is Phi = (1+√5)/2 = 0.5+(0.5×0.5)0.5
Golden ratio Phi is considered to be the ruler for beauty. When it comes to beauty, it is commonly believed that what we perceive as beauty in women and men is based on how closely the proportions of facial and body dimensions come to golden ratio Phi. For this reason, Phi is applied in both facial plastic surgery and cosmetic dentistry as a guide to achieving the most natural and beautiful results in facial features and appearance. More the closer of Phi proportions in human body, more the beauty and attractive the person is. There are many more several golden ratio proportions in face and human body even at anatomical scale.
The measurement from the navel to the toe and the top of the head to the navel is the golden ratio. The mouth and nose are each positioned at golden sections of the distance between the eyes and the bottom of the chin. The total width of the two front teeth in the upper jaw over their height gives a golden ratio. The width of the first tooth from the centre to the second tooth also yields a golden ratio.
Some of the other notable golden ratios in the human face are – (i) Length of face / width of face (ii) Distance between the lips and where the eyebrows meet / length of nose (iii) Length of face / distance between tip of jaw and where the eyebrows meet (iv) Length of mouth / width of nose (v) Width of nose / distance between nostrils (vi) Distance between pupils / distance between eyebrows.
Golden ratio proportions are seen in human hand. Looking at the length of our fingers, each section – from the tip of the base to the wrist – is larger than the preceding one by roughly the ratio of phi.
Animal bodies exhibit similar tendencies, including dolphins (the eye, fins and tail all fall at Golden Sections), starfish, sand dollars, sea urchins, ants, and honey bees. Mollusk (Nautilus Shell) are the most common and studied beings which are associated with Fibonacci Spiral – the manifestation of Golden Spiral in nature. However, not all the mollusk grows at the same scale and size because some of them have been constrained by non-ideal environmental conditions.
It is also observed that Golden Ratio Phi proportion is found in human lungs bronchi network in such a way that in all divisions of bronchi, the proportion of the long bronchus to the short is always Phi proportion. In the human heart, the ratio of the maximum (systolic) pressure to the minimum (diastolic) pressure is equal, on the average, to 1.6, that is, is close to the golden proportion. Surprisingly, golden ratio proportions are also found in human brain waves. It was thrilled to discover that when women are at their most fertile, between the ages of 16 and 20, the ratio of length to width of a uterus is ~1.6 – a good approximation to the golden ratio.
Even the microscopic realm is not immune to Fibonacci numbers and Golden ratio. The DNA molecule, the program for all life, is based on the golden section. A DNA molecule measures 34 angstroms long by 21 angstroms wide for each full cycle of its double helix spiral. 34 and 21, of course, are numbers in the Fibonacci series and their ratio, 1.6190476 closely approximates Phi, 1.6180339. Moreover, double stranded helix DNA has a groove in its spirals, with a ratio of Phi in the proportion of the major groove to the minor groove, or roughly 21 angstroms to 13 angstroms. A cross-sectional view from the top of the DNA double helix forms a decagon which is in essence two pentagons, with one rotated by 36 degrees from the other, so each spiral of the double helix must trace out the shape of a regular pentagon. The diagonal to side ratio of a regular pentagon is equal to the golden ratio Phi.
The golden ratio Phi is also found to be associated with architecture, art and design in many contexts. It is often said that when the building is said to be created in golden ratio proportions, it is sacred architecture. By applying the calculation of the Golden Ratio to a square, architects and designers are able to create the Golden Rectangle, which is believed to have the most aesthetically pleasing proportions to the human eye. The ancient pyramids have always been associated with divinity and Golden ratio proportions, in the form of Kepler triangle, are seen in ~ 4500 years old the Great Pyramid of Giza (Pyramid of Khufu), the oldest of the Seven Wonders of the Ancient World, that was built around 2560 BC.
Phidias, the Greek sculptor, used the Golden Ratio in his work, especially in the construction of sacred Parthenon structure. More modern applications of the Golden Ratio in architecture can be seen in Notre Dame in Paris, the United Nations Headquarters Secretariat building in New York, Taj Mahal in Agra and the CN Tower in Toronto.
We can find many examples of Golden ratio proportions used by master painters. Golden ratio art examples include – Leonardo Di Vinci – Mona Lisa, Vitruvian Man; Botticelli – Birth of Venus; Michelangelo – Holy Family, David; Raphael – Crucifixion; Rembrandt – Self-Portrait; Salvador Dali – The Sacrament of the Last Supper, The Persistence of Memory.
Golden ratio also plays interesting role in music and acoustics. The dimensions of the treasured Stradivarius violins built around 1700 show golden ratio Phi (F) relationships. Some of the most known classical composers used the Golden Ratio and Fibonacci Sequencing in their music pieces, including Bach, Beethoven, Chopin, and Mozart. Some modern composers like Casey Mongoven have explored the Golden Ratio in their music.
Golden ratio is also commonly used in the design of products and logos like Apple logo, Toyota logo and by many major corporation sectors.
Golden ratio relationships are even found in the solar system and universe scale. Some of the surprising golden ratio relations in solar system are – the diameters of the Earth and Moon form a Golden triangle called Kepler Triangle, the distances of the planets from the sun correlate surprisingly closely to exponential powers of golden ratio the beautiful rings of Saturn are very close in dimension to the golden ratio of the planet’s diameter. It is often believed that the Milky Way galaxy, the Andromeda Nebula and the Spiral Galaxy M81 have spiral patterns resembling the golden spiral.
In 2003, curiously enough, NASA released findings from the data collected with the Wilkinson Microwave Anisotropy Probe (WMAP) satellite on cosmic microwave background radiation that mathematical models of a spherical, solid Universe edged by 12 curved pentagons produce the patterns seen in the background radiation without any special fine-tuning. Thus, it concludes that the shape of the Universe would be a Dodecahedron. Dodecahedron is a 3-dimensional Platonic solid which is constructed based on golden ratio. In dodecahedron, the 12 corners become the 12 centres of each of the 12 pentagons that form the 12 pentagonal faces. Thus, altogether, a dodecahedron has 12 pentagonal faces, 20 vertices and 30 edges.
Even today, the Golden Ratio Phi continues to open new doors in our deep understanding of life, relativity, quantum and the universe and Phi plays incredible role in integrating knowledge across a wide variety of fields of study and unveiling a hidden harmony or connectedness in so much of what we see.
Decoding the Holy Symbol of Sanamahi – Ama
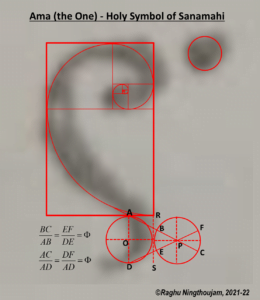
In order to understand whether any meaningful feature is hidden in the holy symbol Ama (the One), the humble writer tries to connect the dots between the sacred symbol, mathematics and science. As it can be seen from the geometry of the holy symbol of Ama (the one) – the divine symbol of Lainingthou Sanamahi has an upper part which is in the form of a spiral and a smaller incomplete circular arc as a tail part. Also, the divine symbol has a dot (like) figure near to the spiral head. The humble writer will try to decipher each portion of the holy symbol in the following sections.
Decoding the Upper Part
The upper part is the main portion of the holy symbol and for decoding any secret attributes in the divine symbol of Sanamahi, the humble writer took the original figure as written in the sacred ancient manuscript –‘Wakoklon Heelel Thilel Salai Amailon Pukok Puya’ written in Meetei-mayek scripts. As can been seen that the upper part of the divine symbol has exquisite spiral-like feature and this was the hint kept hidden in the holy symbol. Then, the humble writer, beginning with a square of proper dimension in proportion with the upper part of the holy symbol, carefully draws a golden rectangle with the standard procedure. After several iterations and exercises, the best golden rectangle which fits to the upper part of the holy symbol of Ama (the One) is chosen to begin with. Then, the self-similarity property of golden rectangle is applied. Denoting the length and breadth of the master golden rectangle as L and B such that L/B = Phi (golden ratio), then, the master golden rectangle is subdivided into a square of side B and another rectangle of length (L-B) and breath B, which turns out to be another golden rectangle. This smaller golden rectangle is again subdivided into another square and another smaller golden rectangle, and the process continues. Now, considering only the squares which have been divided from the respective golden rectangles, for each square, we can draw an inscribed quarter circle with radius equal to the side of that square. Then, by connecting all the inscribed quarter arc circles, Golden Spiral is drawn. Curiously enough, the golden spiral almost exactly fits to the holy symbol of Sanamahi, as it can be seen from the figure – what a magnificent beauty of the radiant symbol of Lainingthou Sanamahi. Thus, it is clearly unveiled that the holy symbol – Ama (the one) has a glorious golden spiral with golden ratios embedded inside. Due to the presence of golden ratio signatures in the golden spiral, the spiral looks so special and appealing to the beholders. The centre of the golden spiral is called the accumulation point of the spiralling squares and is considered to be God’s eye.
Decoding the Tail Part
Having unveiled the hidden signature of a golden spiral signature in the upper portion of the holy symbol of Sanamahi, the humble writer further investigates the tail part of the symbol i.e. the portion after the waist which is the incomplete circular arc portion of the symbol. Unlike the upper part of the holy symbol, this tail part does not reveal hidden features easily and it requires deep investigation.
For decoding this part, with O as the centre of the incomplete circular arc, humble writer draws an inscribed circle such that the extended line RS of the main golden spiral is tangent to the inscribed circle. Then, considering the line RS as the line of symmetry, a mirror-image circle of inscribed circle with centre O is drawn and the point P is the centre of the mirror-image circle. The extended line RS is common tangent to both the symmetrical circles with centres at O and P. The line AOD is the diameter of the inscribed circle with centre O, with A and D being the diametrically opposite points. Now, from the point A, a line ABPC is drawn passing through the centre P of the mirror-image circle and the line ABPC cuts the mirror-image circle at circumferential points B and C as shown in figure. Similarly, another line DEPF is drawn from the point D passing through the centre P of the mirror-image circle, cutting the circle at circumferential points E and F as shown in figure.
Surprisingly, the line ABPC when extended from the point A, is tangent to the golden spiral, as it can be seen in the figure. Similarly, the line DEPF when extended from the point D, is tangent to the incomplete circular arc of the holy symbol which is the tail part of it. And the extended line RS from the golden spiral is the line of symmetry and common tangent to both the circles. This feature is also equally intriguing. Now, from the geometrical constructions of the inscribed circle and its mirror image and the corresponding line segments and ratios, we can prove certain interesting relations as follows:
Since all the radii of a circle are equal and the inscribed and its mirror image circles are symmetrical, we have the following radii relations:
OA = OD = PB = PC = PE = PF = OP/2
Now, applying Pythagoras theorem to the right angled triangle AOP, we get, OA2 + OP2 = AP2 which implies that AP = √5 OA and AB = AP – BP = (√5-1) OA
Therefore, BC/AB = 2 / (√5-1) = (1+√5) / 2 = Phi
Similarly, EF/DE = 2 / (√5-1) = (1+√5) / 2 = Phi
Thus, BC/AB = EF/DE = Phi (golden ratio)
Also, PC + AP = (1+√5) OA
Therefore, AC/AD = (1+√5) / 2 = Phi. Similarly, DE/AD = (1+√5) / 2 = Phi
Thus, AC/AD = EF/AD = Phi (golden ratio)
Combining the above equations, it follows that the ratio i.e.
BC/AB = EF/DE = AC/AD = EF/AD is in golden ratio Phi.
That is, BC/AB = EF/DE = AC/AD = EF/AD = Golden Ratio Phi, from which it is very clear that, amazingly, in addition to the presence of golden ratio (in the form of golden spiral) in the upper main portion of the holy symbol of Sanamahi Ama (the One), the lower portion (tail part) of the holy symbol of Sanamahi is also intricately embodied with hidden golden ratio signatures – what an incredible feature hidden in the tail part of the holy symbol of Lainingthou Sanamahi..!
Decoding the Dot
Now, having unravelled the secret golden ratios both in the upper part and tail part of the figure of Ama – the holy symbol of Sanamahi, let’s see what could be the hidden meaning of the dot-like feature of Ama, located near its head-portion. It is marked as a circle in the figure. Humble writer carefully observes this dot-like figure in the original manuscript of sacred puya ‘Wakoklon Heelel Thilel Salai Amailon Pukok Puya’ and contemplates what could be the secret interpretation behind this dot.
In order to understand the meaning of this dot, we’ll go back to Wakoklon puya. Learned readers may kindly recall the verse of Wakoklon puya that says that in the very beginning of the universe (when time t=0), there was a supreme God Eepung Loinapa Apakpa also called Tingpalpaki Mapu as the Owner (guardian) of the (seed) Universe (Tingpalpa means Universe, Mapu means Owner) and by His desire, He created the universe and everything inside it, from that seed universe. That seed universe is also called the singularity point of the universe, to which everything was contained and from which everything was originated. The singularity point is a solid figure having matter and energy inside it and the supreme God (Sanamahi) was the guardian (owner) of the point (singularity). Since Lainingthou Sanamahi is the guardian (owner), He just stays nearby taking care of the holy point as if both are always together (Loinapa means Together in Eepung Loinapa Apakpa), which is rightly depicted the position of Ama (Sanamahi) and the Holy point (Seed Universe), next to each other. That means, the ultimate creator ‘Eepung Loinapa Apakpa’ (Sanamahi) was always together (Loinapa) with the universe (represented by a dot).
Thus, from the physics point of view, the dot-like structure next to the figure of Ama (Sanamahi) can be interpreted as the Singularity point having mass and energy and hence represented by the solid figure. Also, among the various shapes of geometrical figures, ancient men were fascinated by the shapes of heavenly objects like Sun, Moon and visible Planets which are round (circular) in shape and thus the most popular figure was circle which is the shape of a dot, in 2-dimensions. Science per say, this singularity point is known as Big Bang Singularity according to Big Bang theory of universe. According to Big Bang theory, around 13.8 billion years ago, the entire universe was started from a singularity point which was an infinitesimally small point with infinite density and temperature. And, at this point and moment, the most-sought-after theory of physics i.e. the Grand Unification Theory (GUT) was apparently operating, wherein all the four fundamental forces of nature i.e. gravity, nuclear strong force, nuclear weak force, and electromagnetic force were combined into a single Super force.
However, from the mathematics point of view, the very beginning of the universe, around 13.8 billion years ago, when time t=0, at which the space and time were together as spacetime and there was nothing (0) in the universe and when the universe was a just a point that is a dot which is a figure with zero (0) dimension with no length, no breadth, no height, the singularity point will be best represented mathematically by zero (0). This means that the early universe (the universe at t=0) was like a null (0). Thus, if we have to take mathematics out of the dot-figure, it is just a zero (0) representing the singularity or void state of the universe at time t=0.
Mathematically, this is as equivalent as assigning of zero (0) to dot and one (1) to the holy symbol of Ama (the one). The, what is this? Astonishingly, learned readers may recall that this is nothing but the first two Fibonacci numbers. We know, given the first two numbers 0 and 1, the entire infinite Fibonacci series can be created and the Fibonacci numbers are profusely found in nature. This is how, probably, the entire universe was created by ultimate God Lainingthou Sanamahi (represented by 1) from the Singular Dot (represented by 0), as depicted in Puya. What a mesmerizing feature of the holy symbol of Sanamahi…!
Yet, another intriguing interpretation of the dot-like structure of the figure of Ama could be seen from the angle of the shape of the universe. As seen above, dot is the universe and the numeral figure – Ama (Sanamahi) is the owner of the universe and they are together (Loinaduna lei). Is the shape of the universe really dot-like solid figure? Or, does this dot-like figure also have some hidden golden ratio signature because the immediate holy figure Ama is having secret golden ratio signatures? To address this curiosity, learned readers may recall that universe was contained in the dot – the singularity point and as seen above, in 2003, curiously enough, as per findings of NASA, the shape of the Universe is a Dodecahedron. Dodecahedron is a 3-dimensional geometrical solid football like figure having 12 pentagonal faces which are having golden ratios in each pentagon. Moreover, 3-dimensional solid figure when it is drawn in plain paper, it would be automatically transformed to a 2-dimensional figure like a flat-solid-dot circular in shape. Thus, the possibility exists and it cannot be ruled out that the dot-like structure would subtly be a dodecahedron (the anticipated shape of the universe). However, to be frank, humble writer cannot confidently assert this aspect as the divine author (Maichou) of the Puya has left with the imprint of a dot in the sacred puya, on a 2-dimensional paper.
What About the Size
Learned readers might have carefully observed about the size of the figure of Ama and Dot in the holy symbol of Lainingthou Sanamahi (Ama). The figure Dot is tiny while the figure of Ama is really huge as compared with the Dot. Is the reverse possible? What could be the meaning of this specific relative sizes as if purposefully drawn by the divine author (Maichou) of the Puya? Here is the answer as conceived by the humble writer. As we have seen, as written in sacred puya that the figure of Ama is depiction of the creator Sanamahi and Dot is the universe and together it represents the Holy symbol of Lainingthou Sanamahi as the two entities are always together (Loinapa Apakpa). Since Lainingthou Sanamahi is the ultimate, supreme creator, nothing can be bigger than the supreme. And, however big the universe is, it is just like tiny dot to Him, it is nothing representing nullness (zero – 0) to the creator. Therefore, the divine scholar maichou, having known this truth, has kept tiny Dot and Giant Ama in the symbol of Lainingthou Sanamahi. Hence, the reverse order is not possible.
Golden Ratio and Sanamahi Religion
In the preceding sections, we have seen the astonishing meaning of the holy symbol of Lainingthou Sanamahi in terms of golden spiral, golden ratio proportions and the universe itself. Also, amazingly, the humble writer comes across some interesting contexts of the seemingly appearances of Fibonacci numbers and Golden Ratio proportions in some of the traditional materials of Sanamahi religion, which are discussed in the following sections.
Interesting Numerology
We have seen that Golden Ratio Phi = (1+√5)/2. Thus, the primary numbers in the golden ratio Phi are (1, 2, 5) which are interestingly the Fibonacci numbers. Now, let us see whether any meaningful contexts can be decoded with these numbers Fibonacci golden-ratio numbers (1,2,5) along with the four fundamental mathematical operations viz. addition, subtraction, division, and multiplication i.e. (+, -, ÷, x).
First, let us consider a pair of two numbers at a time i.e. (1,5), (1,2) and (2,5) and applying the basic operations, we can get the following outcomes:
1+5 = 6 (Thawai Manga Miga Thana Taruk) = 1 (Body) + 5 (Senses)
5-1 = 4 (Maikei Mari i.e. 4 directions – North, South, East, West)
1+2 = 3 (Matam Ahum – Mangang, Luwang, Khuman)
2+5 = 7 (Salai 7, Numit Chayon 7, Laipungthou 7, Nonglon Maron 7, Malem Leiron 7, Singli Pafal 7, Lai Nura 7 etc.)
5-2 = 3 (Matam Ahum – Mangang, Luwang, Khuman)
Next, let us consider the 3 numbers at a time i.e. (1,2,5) and applying the basic operations, we can get the following outcomes:
1 x 5 + 2 = 7 (Salai 7, Numit Chayon 7, Laipungthou 7, Nonglon Maron 7, Malem Leiron 7, Singli Pafal 7, Lai Nura 7)
2 x 5 + 1 = 11 (1 Body + 10 Fingers (Khutsa); 1 Body + 10 Toes (Khongsa);
2 x 5 – 1 = 9 (Thonglon 9 of human body – Mit 2, Nakong 2, Naton makhul 2, Chin 1, Khathong 2)
(1+5) x 2 = 12 (12 Months of a year – Sajibu, Kalen, Inga, Ingen, Thawan, Langban, Mera, Hiyangei, Poinu, Wakching, Phairen, Lamta)
(5-2) x 1 = 3 (Matam Ahum – Mangang, Luwang, Khuman)
(5-1) x 2 = 8 (Sungdai Nipan – 8 sub-cardinal points)
Is it just mathematical trick and a coincidence? However, it is amazing relation and equally enthralling.
Nongma Panba And Cheiraoba
In Meetei belief and Sanamahi religion, the first day of a month (nongma panba) is considered to be the day of Lainingthou Sanamahi and commonly worshipped the God. Now, the reason behind this belief is very clear, from the above analysis and interpretation of the figure of Ama (the one) that the numeral figure one (unity-Ama) is the manifestation of Lainingthou Sanamahi and vice-versa and Lainingthou Sanamahi stands in the form of a numeral figure one (Ama) along with a dot signifying universe and golden ratios are embedded inside it.
In the similar context, celebration of Cheiraoba (new year) on the first day of Sajibu month i.e. Sajibu nongma panba Cheiraoba is the correct day of celebration of Cheiraoba. This is because, Ama (one) – nongma panba (first day) is the day of Lainingthou Sanamahi and the devotees worship Lainingthou Sanamahi on Nongma panba (one). Any other day, apart from nongma panba, cannot represent Lainingthou Sanamahi and Cheiraoba on other days (like middle of the month) cannot truly represent Cheiraoba in Sanamahi religion. This means that simply, if you are devotee of Lainingthou Sanamahi, nongma panba cheiraoba is the right one.
Golden Ratio in Design
In Sanamahi religion, Khamen Chatpa is a special cloth having its divine connection with its origin and design. It is a traditional loincloth (pheijom) worn by men, with various patterns stamped on it. It is believed that some of the patterns are adopted from ibudhou Pakahangba – the brother of Sanamahi. The khamen chatpa is especially worn by men like Amaibas, Pena singers, during the various auspicious occasions including Lai Haraoba.
Another traditional cloth, worn by women in Manipur state (Kangaleipak), is Phanek Mapan Naibi or Phanek Mayek Naibi. The phanek is revered as a sacred garment, adorned with age-old divine beliefs and myths. In Phanek Mapan Naibi, the motif is to imprint certain design/patterns along the borders (mapan) of the cloth. Amongst the Phanek Mapan Naibi desigs, especially, Khoi Mayek is interesting in terms of its design and patterns.
It is interesting to note that humble writer observes golden spiral (like) patterns in the designs of Khamen Chatpa and Khoi Mayek patterns of Koi Mayek phanek mapan naibi. Whether the special privilege and power of these clothes is attributed to the presence of Ama-like (Sanamahi) patterns with golden ratio embedded. Whether the concept of golden ratio (spiral) was used in the design of this Meetei traditional cloths is naturally curious and scientifically arousing.
Symbol of Pakhangba
Learned readers may be aware of the flagship symbol of Universal Friendship Organization (UFO) – locally known as Satjal. The symbol stands in the form of a serpent dragon with a double-sided spiral pattern, which represents ibudhou Pakhangba (brother of Sanamahi) as a popular belief. Keeping aside whether Pakhangba is represented as serpent or not, the symbol of Satjal is quite interesting in the context that it has beautifully embedded golden spiral patterns and the symbol of Ama (Sanamahi) in both ends. To the humble writer, the double-sided pattern of Satjal is more appealing to be of the numeral mari (four), rather than a serpent dragon, as mari (four) also embodies golden spiral in both ends. The point is that whether the concept of golden ratio (spiral) was used in the design of this Satjal logo is scientifically intriguing.
Back to Puya Again and Epilogue
As we have seen that the sacred ancient text ‘Wakoklon Heelel Thilel Salai Amailon Pukok Puya’ says that in the very beginning (when t = 0), when there was nothing in the cosmos, a Supreme God called ‘Eepung Loinapa Apakpa’ was there. The deathless ‘Eepung Loinapa Apakpa’ was also known as ‘Tingpalpa Mapu’ and He has incarnated as Lainingthou ‘Sanamahi’. The meetei mayek alphabets and numerals have been born out His anatomy. Puya further says that, ‘Eepung Loinapa Apakpa’ aka ‘Tingpalpa Mapu’ aka Lainingthou ‘Sanamahi’ stands in the form of mathematical figure Ama (the one) and thus the divine figure Ama is considered to be the Holy Symbol of Sanamahi.
Mathematically, the holy symbol of Sanamahi Ama – representing 0 and 1 can be correlated to the first two Fibonacci numbers from which infinite Fibonacci series is created and thus the holy figure Ama symbolizes the enormous power of generation acting on 0 and 1. Also, Fibonacci number intricately contains amazing number called golden ratio Phi in it.
We have seen that in the history of mankind, Golden Ratio Phi is a single mysterious number which had pondered great thinkers of all disciplines like Mathematicians, Scientists, Artists, Historians, Architects, Musicians, Psychologists, Mystics and Theologians, over centuries over its ubiquity and appeal. Golden ratio is considered to be divine and God-like because of its ubiquity property that it is found almost everywhere, in art, architecture, plants, human beings, animals, science, mathematics, DNA, solar system and cosmos and what not, like a God who is omnipresent. Also, Golden ratio is regarded to be the most exquisite extant and is called ‘Tool of God’ used to design/create the universe. Among numbers, it is the most irrational number having infinite number of decimals but not repeating like God is infinite. Also, interestingly, Golden ratio is the only number which can be exclusively expressed in terms of infinite 1’s as continued fraction as follows:
F = [1;1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1………..]
Also, curiously enough, we have seen that the holy symbol of Sanamahi Ama has hidden golden spiral and golden ratio signatures in all respects in it. The holy symbol exactly stands in the form of a golden spiral with embedded golden ratio proportions in the tail part as well.
In this article, humble writer tries to bring mathematics out of the holy symbol of Sanamahi that is Ama and its divine beauty. In this effort, an honest attempt has been made to bring out meaningful feature from the holy symbol. Also, it is to be noted that one cannot draw a golden spiral or golden ratio proportions with compass and ruler. Since the sacred puya was a manuscript and written by the divine scholar (maichou), without compass and ruler, the exactness and precise accuracies cannot be expected. However, sufficient hint was available and it was kept like a puzzle. Humble writer examines the centuries-old puzzle under the lens of mathematics and science and solved the mystery which was kept concealed in the sacred Puya.
Also, having unravelled the hidden features and intricacies of the holy symbol of Sanamahi, the humble writer firmly believes that this exercise will set the way forward to accurately design the holy symbol of Sanamahi in exact golden ratio proportions and standardization of the divine symbol henceforth. This will be a significant impact in bringing out the correct and true holy symbol of Sanamahi in desired proportions, as depicted in Puya.
Another interesting aspect is the apparently appearing golden ratio in Khamen Chatpa fee, Phanek Mapan Naibi, Satjal Logo, Symbol of Pakhangba. Many more such interesting golden ratio features may be lying hidden in ancient treasures. Humble writer feels that the aesthetic architectures like Kangla, Temple of Nongda Lairen Pakhangba inside Kangla would have golden ratio proportions and this exercise is left to the researchers as topic(s) of their research.
Interestingly, a subtle relation between Golden Ratio Phi and Ama can be seen from the continued fractions of Ama as:
Phi = [Ama; Ama, Ama, Ama, Ama, Ama, Ama, Ama, Ama…..]
Which means that golden ratio Phi has divine Ama and vice-versa. A probable reason behind the golden ratio as mysterious number….!!
If we see the etymology of the word Tingpalpa Mapu as mentioned in puya, Tingpalpa Mapu = Tingpalpa (Universe) Mapu (Owner), means there must be a universe and there must be an owner- which means that there are two entities that are exactly seen in the symbol Ama. The Dot is the universe (seed universe, initial singularity, represented by 0) and 1 is the owner (Sanamahi) – the Super singularity, the quest of science before the Big Bang event! The two entities symbolize 0 and 1 – the first Fibonacci numbers, which have generated the infinite series. Since the two entities, separately, does not have any meaning, they have to be co-existed always and together represents the symbol of Sanamahi, which can also be understood from the another epithet of Tingpalpa Mapu i.e. Eepung Loinapa Apakpa. Since Eepung Loinapa Apakpa aka Lainingthou Sanamahi is the guardian (owner), He just stays nearby taking care of the holy point as if both are always together (Loinapa means Together in Eepung Loinapa Apakpa), which is rightly depicted the position of Ama (Sanamahi) and the Holy point (Seed Universe), next to each other. That means, the ultimate creator ‘Eepung Loinapa Apakpa’ (Sanamahi) is always together (Loinapa) with the universe (represented by a dot).
As we have seen, as written in sacred Puya that the figure of Ama is depiction of the creator Sanamahi and the figure of Dot is the universe and the two figures together it represents their coexistence (Loinapa Apakpa) that the two entities are always together. ( haiba saktamsi Lainingthou Sanamahi na mapu ama oina tingpalpabu ngak-senduna adum loinaraga leibagi saktamni.)
Golden ratio is regarded to be the secret of the universe, nature’s path of least resistance and maximum performance and the golden key to the cosmos. It is often believed that universe is governed by golden ratio. The Supreme God Lainingthou Sanamahi has manifested to the most precious figure of Ama (the One) and the most astonishing number – Golden ratio is embedded in Ama in all respects, which symbolizes Lainingthou Sanamahi. The pristine symbol Ama is equally as fascinating as Sanamahi – the creator.
This is the divineness of Ama and all these complexities and magnificent beauty have been kept concealed in ancient text – Wakoklon Puya. Meetei Puya will ever remain as unfathomable treasure of all time and more research is required to unearth various breath-taking discoveries.
The Golden Ratio mathematics behind the intricacies of the holy symbol of the Sanamahi and the discretions thereof, along with the scientific significance and mathematical essence of the spectacular divine symbol of Lainingthou Sanamahi has once again affirmed that Lainingthou Sanamahi is the ultimate, supreme God and creator of Universe and the Holy symbol of Sanamahi – Ama (the One) which signifies the Coexistence of the Creator (Sanamahi) and Universe (Dot) in glorious Golden Ratio Proportions, will remain as the most revered divine symbol in Sanamahi religion.
(Raghu Ningthoujam is a scientist currently serving at Indian Space Research Organization (ISRO) and alumni of IISc Bangalore, IIT-Guwahati, DM College of Science, Imphal. He can be contacted at [email protected]. Views expressed are his own.)
